Triangle Mesh Simplification
The objective of the mesh simplification problem is to reduce the number of vertices in a triangle mesh while retaining the original shape and appearance of the mesh as closely as possible. Generally you can think about the problem in terms of removing unnecessary or redundant triangles until the desired vertex count is attained. The purpose of this kind of algorithm is to increase rendering performance, either by generating LODs for relatime applications such as video games, or by reducing the size of meshes generated by 3D scanning or high-res sculpting applications, where meshes containing millions of triangles are not uncommon. In 2014 I evaluated and implemented serveral such algorithms for my bachelors thesis.

Bunny mesh simplified to 1% of its original size. The Original size of this mesh is 35947 vertices.
Academic research of mesh simplification algorithms peaked in the 90s and early 2000s when several important algorithms were published. Of course back then, demand for this was high due to limited hardware power.
For the thesis I did my research on the existing literature, but only focused on implementing and evaluating two papers: The landmark paper “Surface simplification using quadric error metrics” by M. Garland and P. S. Heckbert (1997) and “Image-driven Simplification” by P. Lindstrom and G. Turk (2000). Although the latter seems more unconventional and harder to implement efficiently, I very much liked the idea behind it. As a side note, I believe the paper may have inspired some commercial mesh simplification solutions developed many years later, but I don’t have much evidence supporting this. Anyways, some minor improvements from other papers also made their way into the project.
The first method works by sequentially contracting vertex pairs based on an elegant and easy to compute error metric that measures how much the contracted vertex changes the local surface shape. This metric is 0 when the triangles surrounding a vertex pair all lie on the same plane - this pair would be selected first for contraction as it adds nothing to the shape of the mesh.
For image-driven simplification, the cost (and therefore the order) of edge collapses is determined by rendering the mesh from 20 different angles and computing the difference between the resulting set of images and the set of images rendered before the edge collapse. This approach preserves visual appearance much better for otherwise “challenging” meshes in low-triangle scenarios. As a bonus, it can also remove triangles that are not visible from the outside of a mesh.
Making the second approach perform quickly was way more challenging than the already efficient method by Garland and Heckbert. First, to save on GPU and CPU memory bandwith, I had to develop a method by which only the part of the image that was affected by an edge collapse is rendered, which I achieved by projecting affected vertices to screen-space and computing a bounding rectangle, then reading out only pixels in the bounding rectangle from the framebuffer. This was a good start but didn’t help for the other problem: you still needed to render entire mesh 180000 times just to reduce 1000 vertices, which is clearly very expensive. I used the so called “triangle bucket” data structure 1 to restrict the set of rendered vertices to a minimum. After adding multi-threading, I got a total running time improvement by another factor of six. Nice!
The results
In low-poly situations, the image driven simplification could often preserve actual shape and appearance much better than the quadric error simplification. This is best demonstrated with the mesh of a locomotive in the images below.
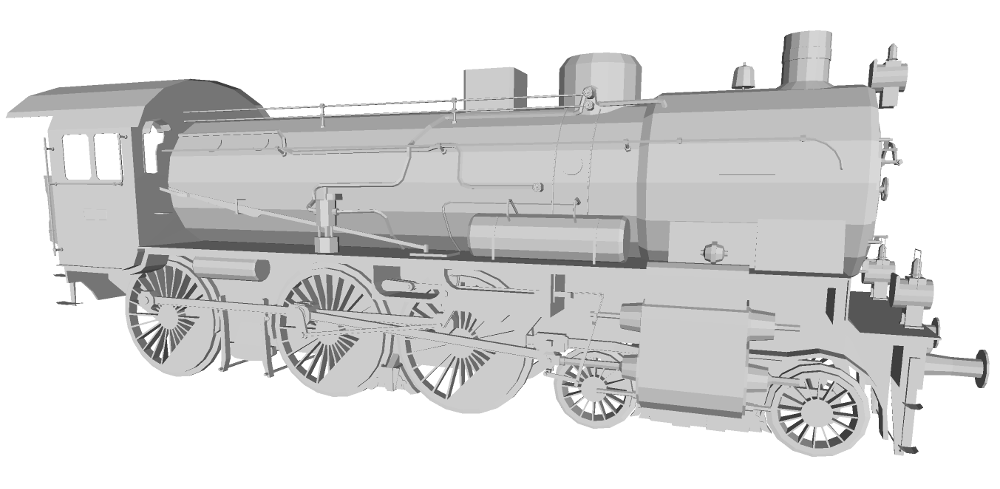
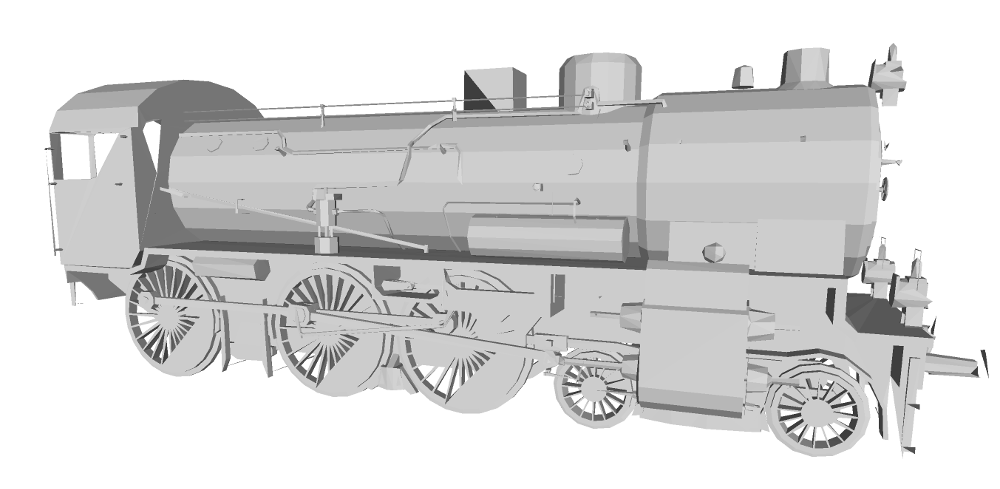
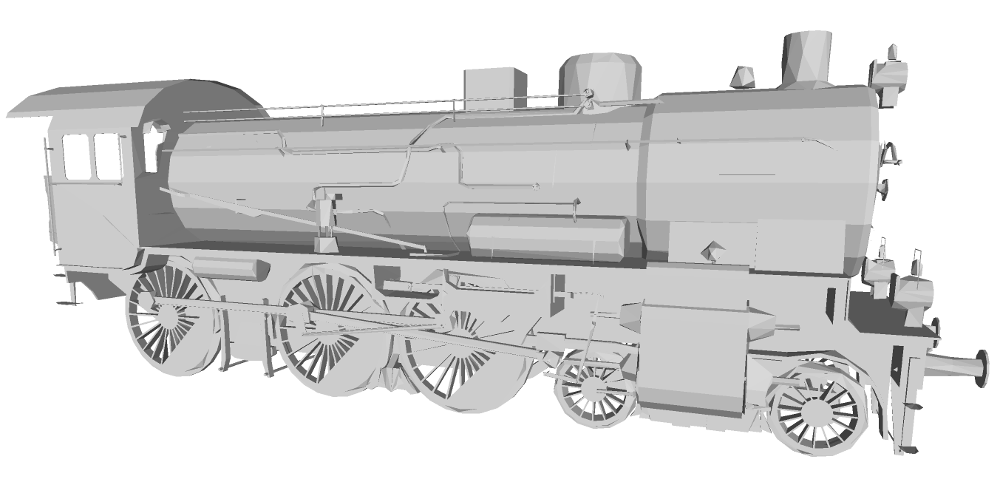
An already lowpoly mesh (left) simplified using Garland and Heckbeck quadric error metric (middle) and image-driven simplification (right).



Bunny mesh pre-simplified to 5000 vertices (left), to 400 vertices (middle) and 400 vertices with image-driven simplification (right). From an appearance standpoint, the image-driven simplification resembles the original mesh more closely.
Performance
A 3 609 600 vertex mesh (the XYZ RBG Asian Dragon) could be reduced to 10% of its size in just under 80 seconds on a 3 GHz processor (single threaded) using error quadrics. Image-driven simplification performed at an average reduction rate of 150 vertices per second when starting from 7000 and reducing to 700 vertices. 2
What else
Seeing how far I could push performance optimizations was an interesting challenge for me. For instance, aside from implementing the algorithms, I also wrote a priority queue implementation that can perform optimally for mesh simplification, where you have around 30-50 times more updates than find-minimums. In theory, the fastest heap should be the Fibonacci Heap here, with an increase-key operation in O(1) and decrease-key in O(log n). As I confirmed experimentally, the Pairing Heap is faster in practice despite having worse guarantees on the update complexity. My own implementation of the pairing heap beat some other implementations in terms of performance I tested at the time (I remember testing against all of the heap implementations in the Boost library).
Of course course plain, untextured meshes are not so typical nowadays. It wasn’t part of my thesis, but it is possible to extend the methods to work with textured meshes, where preserving shape is no longer the only criterion; instead, preserving textured appearance, for example by minimizing texture distortion, is required as well.
Note: This is a highly compressed overview. Many details are omitted.
- P. Lindstrom and G. Turk “Fast and memory efficient polygonal simplification” (1998) [return]
- Pre-simplifying the mesh using the much faster first method to a lower vertex count where it has a performance advantage and no disadvantage on visual appearance, then applying the image-driven algorithm to reduce it even further. [return]